Spearman’s Rank Correlation Coefficient
[this page | pdf | back links]
Spearman’s rank correlation coefficient is defined as the
normal (i.e. Pearson) correlation coefficient but applied to the ranks of the
observations in the two data series. Thus if the two series are 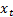 and
and 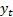 and the
ranks (1 = lowest, …,
and the
ranks (1 = lowest, …, 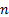 = highest)
of the elements in the two series are
= highest)
of the elements in the two series are 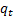 and
and 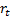 respectively
then:
respectively
then:
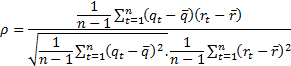
If observations can be tied then it is usual to assign a
rank to each of the tied observations which is the mean of what their ranks
would otherwise have been.
A Spearman correlation of 1 arises when the two variables
being compared are monotonically related, even if their relationship is not
linear.
See MnSpearmanRankCorrelation
or MnSpearmanRankCorrelations
for Nematrian web functions that can be used to calculate Spearman rank
correlation coefficients.