High resolution extended image near field
optics
4. Exact radiating solutions to Maxwell’s
equations in the presence of idealised plane mirrors
[this page | pdf | references | back links]
Copyright (c) Malcolm
Kemp 2010
Return
to Abstract and Contents
Next
page
Consider now the behaviour of inwardly and outwardly
radiating (magnetic) dipoles in the presence of an idealised plane mirror, i.e.
the solution, say, in the half space 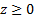 arising from a dipole whose
origin in Cartesian coordinates
arising from a dipole whose
origin in Cartesian coordinates 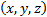 is
given by
is
given by 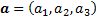 (
(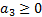 )
and whose direction is given by
)
and whose direction is given by 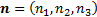 if
there is:
if
there is:
(a) A vacuum in the
region 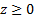 ; and
; and
(b) A perfectly conducting
plane mirror at 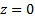 .
.
As Born & Wolf (1980) explain, the exact boundary
condition satisfied on the plane 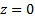 is that the component of
is that the component of 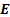 tangential
to
tangential
to 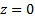 is zero.
is zero.
Now let 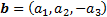 and
and
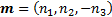 .
The reason we focus on magnetic rather than electric dipoles
using the terminology in Section
3 is that the superposition of two such equal magnitude and in-phase
dipoles, one emanating at
.
The reason we focus on magnetic rather than electric dipoles
using the terminology in Section
3 is that the superposition of two such equal magnitude and in-phase
dipoles, one emanating at 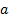 pointing in direction
pointing in direction 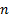 and the other
emanating at
and the other
emanating at 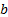 and pointing in the direction
and pointing in the direction 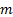 then exactly
satisfies the required boundary condition at
then exactly
satisfies the required boundary condition at 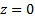 . Suppose we
write this superposition as:
. Suppose we
write this superposition as:
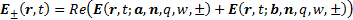
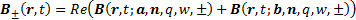
It exactly satisfies the boundary condition because at 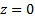 we have
we have 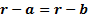 and
and
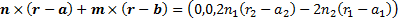 ,
if
,
if 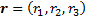 in
Cartesian coordinates. So the
in
Cartesian coordinates. So the 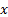 and
and 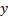 components of
the electric field at
components of
the electric field at 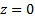 are both zero and
are both zero and 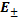 is
thus exactly perpendicular to the mirror.
is
thus exactly perpendicular to the mirror.
Consider further the special case of the above where 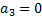 and
and
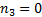 .
We then have
.
We then have 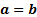 and
and
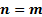 ,
the dipole is emanating from the plane mirror itself and the solutions take the
form:
,
the dipole is emanating from the plane mirror itself and the solutions take the
form:
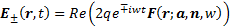
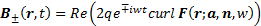
Surfaces of constant phase for this special case are
hemispheres centred about 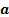 .
The direction and amplitude of the real physical values of
.
The direction and amplitude of the real physical values of 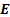 on
each such hemisphere then have the form
on
each such hemisphere then have the form 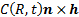 ,
i.e.
,
i.e. 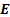 is
perpendicular to both the direction of the corresponding radius vector and the
direction of the dipole and has a maximum amplitude proportional to the sine of
the angle between these two vectors.
is
perpendicular to both the direction of the corresponding radius vector and the
direction of the dipole and has a maximum amplitude proportional to the sine of
the angle between these two vectors.
Consider also the situation where we have the special case
solution form as above and we place a perfectly conducting metallic
hemispherical mirror placed at 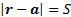 (in
the region
(in
the region 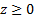 ) for some constant
) for some constant 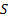 . As
. As 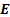 is
exactly tangential to each such hemisphere, any exact outwardly
radiating (magnetic) dipole from
is
exactly tangential to each such hemisphere, any exact outwardly
radiating (magnetic) dipole from 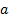 will strike the hemisphere, be
reflected with a 180 degree phase transition and create exactly the right
boundary conditions to create an exact inwardly radiating (magnetic dipole).
will strike the hemisphere, be
reflected with a 180 degree phase transition and create exactly the right
boundary conditions to create an exact inwardly radiating (magnetic dipole).
If the hemisphere was centred at 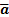 ,
some point on the plane mirror not far from
,
some point on the plane mirror not far from 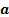 ,
then outwardly radiating dipoles from
,
then outwardly radiating dipoles from 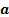 would
not have the right characteristics to generate the exact boundary conditions
needed for an equivalent inwardly radiating dipole, at least not one that
radiates back to
would
not have the right characteristics to generate the exact boundary conditions
needed for an equivalent inwardly radiating dipole, at least not one that
radiates back to 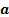 .
However, any dipole emanating from
.
However, any dipole emanating from 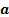 that
bounced a second time off the plane mirror and then of the hemispherical mirror
would then have the right characteristics, to first order, to create the
required boundary conditions. So, if
that
bounced a second time off the plane mirror and then of the hemispherical mirror
would then have the right characteristics, to first order, to create the
required boundary conditions. So, if 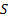 is sufficiently large compared
to
is sufficiently large compared
to 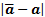 then
the layout would again create an arbitrarily accurate inwardly radiating
(magnetic) dipole with destination
then
the layout would again create an arbitrarily accurate inwardly radiating
(magnetic) dipole with destination 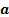 .
.
NAVIGATION LINKS
Contents | Prev | Next